割引現在価値の学び方（その１）

−会計配分と割引現在価値−

１）２つの計算系

２）割引現在価値と会計計算：２つの系

３）３つのケースによる学習

�@リース会計

�A満期保有目的債券

�B貸倒懸念債権

１）２つの計算系

２つの計算系−会計配分と価値評価

１　系�Uがストック志向：利益計算よりもまずは実態・リスクの開示会計（財務透明性）

２　系�Uの“台頭”：「包括利益」なる利益概念…２つの系の“交錯”と“調整”の場

３　計算基点（当初認識時vs.特定時点）の相違

４　将来キャッシュフローが何らかのかたちで確定しているか、それとも不確定か（確率変数）

５　会計志向のハイブリッド：動態論的会計観からさらに企業価値的会計観へ

２）割引現在価値と会計計算：２つの系

３）３つのケースによる学習

�@ケース１：リース会計

Ａ社（決算日は12月31日）は×１年１月1日に、以下の条件により機械のリース契約を結び、即日使用を開始した。なお、当該リース契約はファイナンス・リース契約であり、リース期間終了後の所有権に関して無条件に移転するものとは認められない。

リース条件：イリース期間：契約日より5年間、ロ支払リース料：年間400,000円(毎年12月31日支払)、ハ借手の見積現金購入価額：1,700,000円、ニ借手の追加借入利子率：年５％

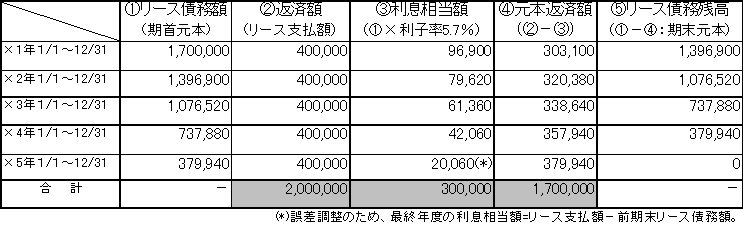
〈要点：ケース１〉

�@ �@リース支払総額の借手の利子率５％による割引現在価値＝1,731,790＞見積現金購 入価額＝1,700,000

�A リース資産の計上価額（元本）＝�@の小さい方＝1,700,000

�B 利息相当額のための利子率の計算：リース支払総額の割引現在価値＝�Aとなる割引率（利子率）　　　　　　　　

例：ｒ≒5.7％ [400,000／(1＋ｒ)＋400,000／(1＋ｒ)^２＋400,000／(1＋ｒ)^３＋400,000／(1＋ｒ)^４＋400,000／(1＋ｒ)⁵≒1,700,000となるｒの値]

�C 毎期のリース支払額の元本分と利息分の分解：利息分＝期首元本（ＰＶ）×�Bの利率

例:　第１期＝�Aの元本×�Bの利子率＝1,700,000×5.7％＝96,900＝利息分、元本返済分＝リース支払額400,000−96,900＝303,100

�D 期末元本＝期首元本−�Cでの元本返済分

〈仕訳：ケース１〉

・リース開始日：　（借）機械装置　××（�A）　　　　　　（貸）リース債務　××

・リース料支払日：（借）リース債務　××（�Cの元本分）　（貸）現金預金　××

　　　　　　　　　　　支払利息　　××（�Cの利息分）

�Aケース２：満期保有目的債券

Ａ社（12月決算）は、×１年１月１日に以下に示す既発行のＢ社社債を9,650,000で取得した。この債券は、満期まで所有する意図をもって保有するものである。なお、取得価額と債券金額（額面）との差額（取得差額）は、すべて金利の調整部分（金利調整差額）である。

イ額面：10,000,000、ロ満期：×４年12月31日、ハ利子率：年利５％、ニ利払日：毎年12月末日（年１回）

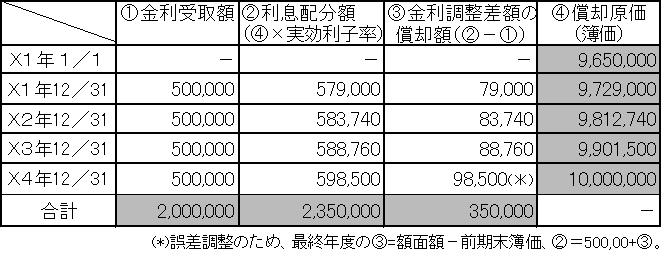
〈要点：ケース２〉

�@ 実質的な利息総額＝受取が確定している各期の契約利息＋取得時の金利調整差額（額面額と取得価額との差額）

例：2,000,000＋(10,000,000−9,650,000)＝2,350,000

�A 実効利子率＝確定している将来キャッシュ・インフロー（契約利息＋額面額）の現　

在価値が（額面以下の）購入価額に等しくなる割引率

例：ｒ≒６％ [500,000／(1＋ｒ)＋500,000／(1＋ｒ)^２＋500,000／(1＋ｒ)^３＋10,500,000／(1＋ｒ)^４≒9,650,000となるｒの値]

�B 利息総額の期間配分＝期首簿価（期首ＰＶ）×実効利子率

例：第１年度は9,650,000×0.06＝579,000

�C 金利調整額の配分＝�B−契約利息

例：第１年度は579,000−500,000＝79,000

�D 簿価の計算＝前期末簿価＋�Cの利息配分額

〈仕訳：ケース２〉

・取得日：（借）満期保有目的債券　××（購入価額）　（貸）現金　××

・決算日：（借）現金　××（契約利息）　　（貸）有価証券利息　××（�B）

（利払日） 　 満期保有目的債券　××（�C）

　・満期日：（借）現金　××　　　　（貸）満期保有目的債券　××（額面額）

�Bケース３：貸倒懸念債権

Ａ社がＢ社に対し有する債権金額1,000,000、約定利子率年５％（年１回払い）、残存期間５年（期限一括返済）の債権について、Ｘ１年３月31日の利払後にＢ社から条件緩和の申し出があり、Ａ社は、約定利子率を年２％に引き下げることに合意した。

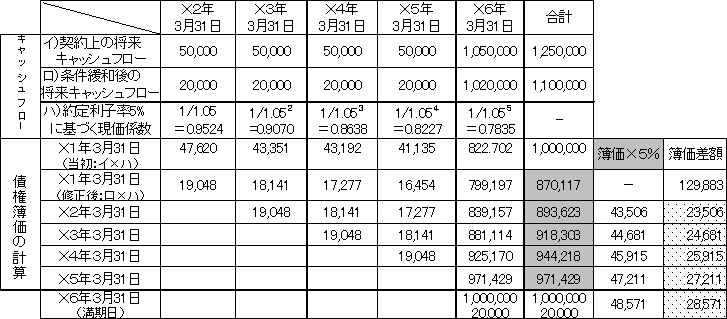
〈要点：ケース３〉

�@ 債権金額1,000,000

�A 債権金額と毎期の当初契約の受取利息（５％）50,000のＰＶ＝�@

例：Ｘ１年度末のＰＶ＝1,000,000、…、Ｘ５年度末のＰＶ＝（50,000＋1,000,000）／1.05＝1,000,000

�B 債権金額と毎期の修正後契約利息（２％）20,000のＰＶ（ただし割引率は当初の　

利子率５％）

例：Ｘ１年度末（修正時）＝￥870,117、Ｘ２年度末＝893,623、

�C 貸倒見積高＝�@−�B（修正時：Ｘ１年度末）

例：1000,000−870,117＝129,883（貸倒引当金繰入額）

�D 毎期の受取利息＝�B期首簿価（期首ＰＶ）×当初の利子率５％　

例：Ｘ２年度末＝870,117×0.05＝43,506

�E 簿価の増価額＝�D−修正後契約利息20,000＝�BのＰＶの期間差額

　　　例：Ｘ２年度末＝43,508−20,000＝23,506＝893,623−870,117

〈仕訳：ケース３〉

・条件緩和時：（借）貸倒引当金繰入額　××（�C）　　　（貸）貸倒引当金　××

・決算日（第１法）：（借）現金預金　××（修正契約利息）　（貸）受取利息　××（�D）

　　　　　　　 　　　　貸倒引当金　　××（�E）

・　〃　(第２法）：（借）現金預金　××（修正契約利息）（貸）受取利息　××

　　　　　　 　　　　　貸倒引当金　　××（�E）　　　　貸倒引当金戻入益　××

３つのケースの要約

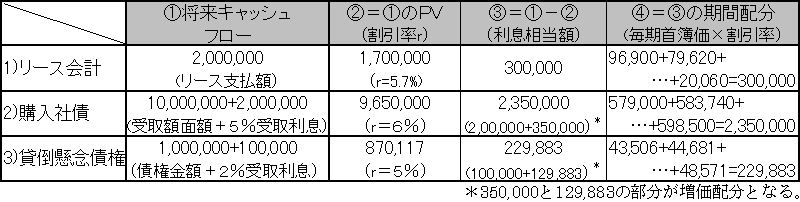
＊より詳しくは、ホームページの「学会・セミナー」の「資産化と利子配分」、および拙稿「割引現在価値と会計配分」（『経営研究』第53巻第３号、2002年11月）、その続編「割引現在価値と価値評価」（予定稿）を参照してください。

（2002年10月）