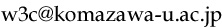２次元多様体（2-manifold, surface）

例

• 2次元球面 S² は閉2次元多様体である。
• 2次元球体 B² は2次元多様体である。B² を円盤又はディスク（disk, disc）という。境界 ∂B² は 円周 S¹ に同相である。 ディスクから境界を除いて得られる多様体 B² - ∂B² を開円盤又はオープンディスク（open disk）という。
• ２枚のディスク B²₁, B²₂ をそれぞれの境界 ∂B²₁ 及び ∂B²₂ で貼り合せると 2次元球面 S² が得られる。
• 2次元球面 S² から２枚の小さなオープンディスクを取り除いて得られる多様体をアニュラス（annulus）という。アニュラスは、直積 S¹×B¹ = { (x,y) | x∈S¹, y∈B¹ } の構造を持つ。
• 2次元球面 S² から３枚の小さなオープンディスクを取り除いて得られる多様体をパンツ（pants）という。
• 一般に、2次元球面 S² からn枚の小さなオープンディスクを取り除いて得られる多様体を平面的曲面（planar surface）という。
• 1次元球面の直積で得られる多様体 S¹×S¹ をトーラス（torus）といい、一般に T² で表す。
• ディスク B² = { (x₁, x₂)∈R² | x₁² + x₂² ≦ 1 } の境界 { (x₁, x₂)∈R² | x₁² + x₂² ＝ 1 } の対心点 (x₁, x₂) と (-x₁, -x₂) を貼り合わせて得られる2次元多様体を射影平面（projective plane）といい、一般に P² で表す。（射影平面）
• 射影平面から1枚の小さなオープンディスクを取り除いて得られる多様体をメビウスの帯（Mobius band）という。
• 2つのメビウスの帯をそれらの境界で貼り合わせて得られる閉2次元多様体をクラインの壺（Klein bottle）という。 （クラインの壷） （クラインの瓶）

向き付け可能（orientable）

2次元多様体 X をいくつかの3角形の和に分割する。各3角形に向きを付け、各辺においてキャンセルするようにできるとき、X は向き付け可能（orientable）という。X が向き付け可能でないとき、向き付け不可能（non-orientable）という。

2次元球面やトーラスは向き付け可能であり、メビウスの帯やクラインの壺は向き付け不可能である。

連結和（connected sum）

X₁, X₂を2次元多様体とし、D₁⊂ int X₁, D₂⊂ int X₂をディスクとする。 ∂D_i = S_i とおくと、S_i は円周である。 このとき、同相写像 S₁ → S₂ によって、S₁ と S₂ を同一視して X₁ - int D₁ と X₂ - int D₂ を貼り合わせる。 この結果得られる2次元多様体 X を X₁とX₂の連結和（connected sum）といい、X₁#X₂で表す。 逆にこのとき、X は X₁とX₂ に分解（decomposition）されるという。

2次元多様体 X の任意の分解 X = X₁#X₂ に対して、X₁ と X₂ の少なくとも一方が2次元球面となるとき、X は素（prime）であるという。 ただし、2次元球面は素ではないと定める。

種数（genus）

g 個のトーラス T²₁, …, T²_g の連結和で得られる閉2次元多様体 F_g = T²₁ # … # T²_g を種数 g の向き付け可能閉曲面（genus g orientable surface）という。g=0 のとき、F₀ = S² と定義する。

h 個の射影平面 P²₁, …, P²_h の連結和で得られる閉2次元多様体 N_h = P²₁ # … # P²_h を種数 h の向き付け不可能閉曲面（genus h non-orientable surface）という。

F_g から b 枚の小さなオープンディスクを取り除いて得られる曲面を種数gの bつ穴あき向き付け可能曲面（genus g b-punctured orientable surface）といい、F_{g, b} で表す。

N_h から b 枚の小さなオープンディスクを取り除いて得られる曲面を種数hの bつ穴あき曲面（genus h b-punctured non-orientable surface）といい、N_{h, b} で表す。

定理（2次元多様体の分類定理）

任意の連結な閉2次元多様体は、次のいずれかに同相である。

一般に、任意の境界成分数 b の連結なコンパクト2次元多様体は、次のいずれかに同相である。

Copyright (C) Makoto Ozawa. All Rights Reserved.