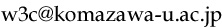
結び目 K の正則図形において、任意の点から K を一周辿るとき、交差が上下交代に現れる正則図形を交代正則図形(alternating diagram)という。 正則図形をもつ結び目を交代結び目(alternating knot)という。
K を交代結び目とし、F を S3 - K 内の圧縮不可能な閉曲面とする。 このとき、次を満たすディスク D が存在する。
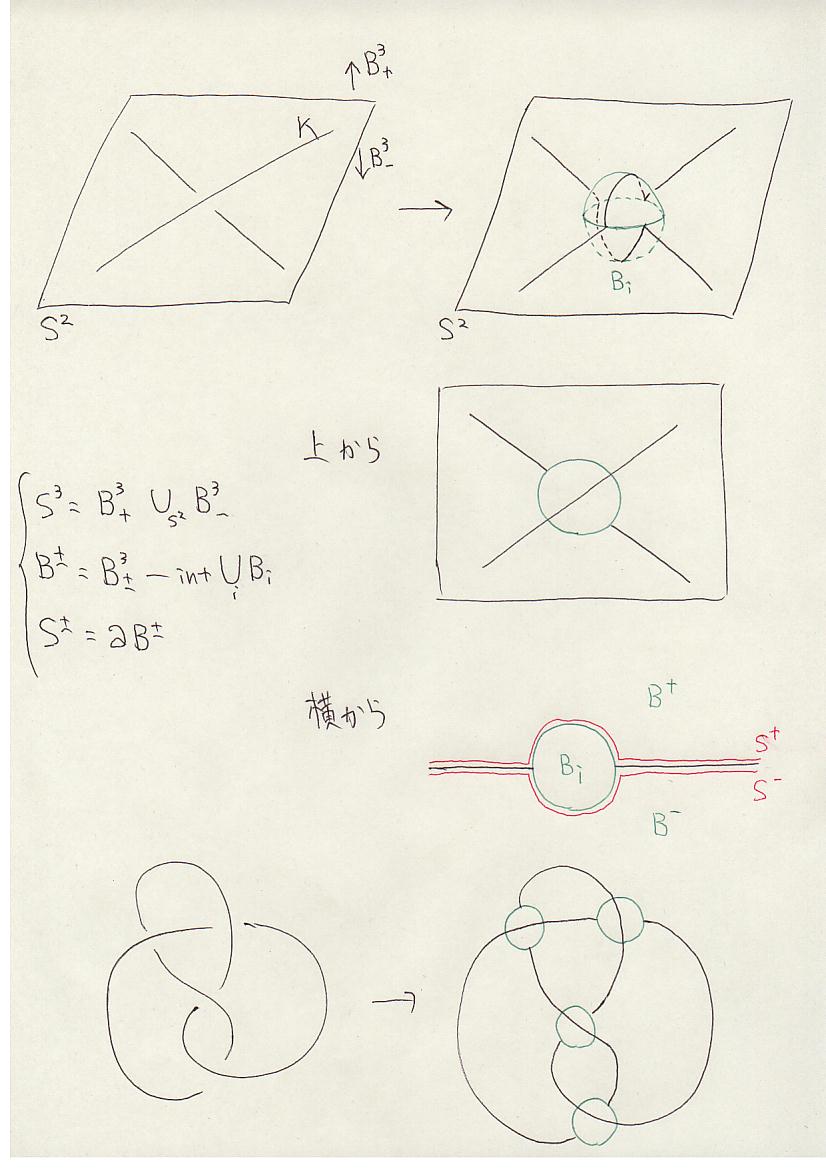
まず、K の交代図形を S2 上に描き、各交点に3次元球体 Bi を下図のように挿入する。

F を変形して、次を満たすようにできる。
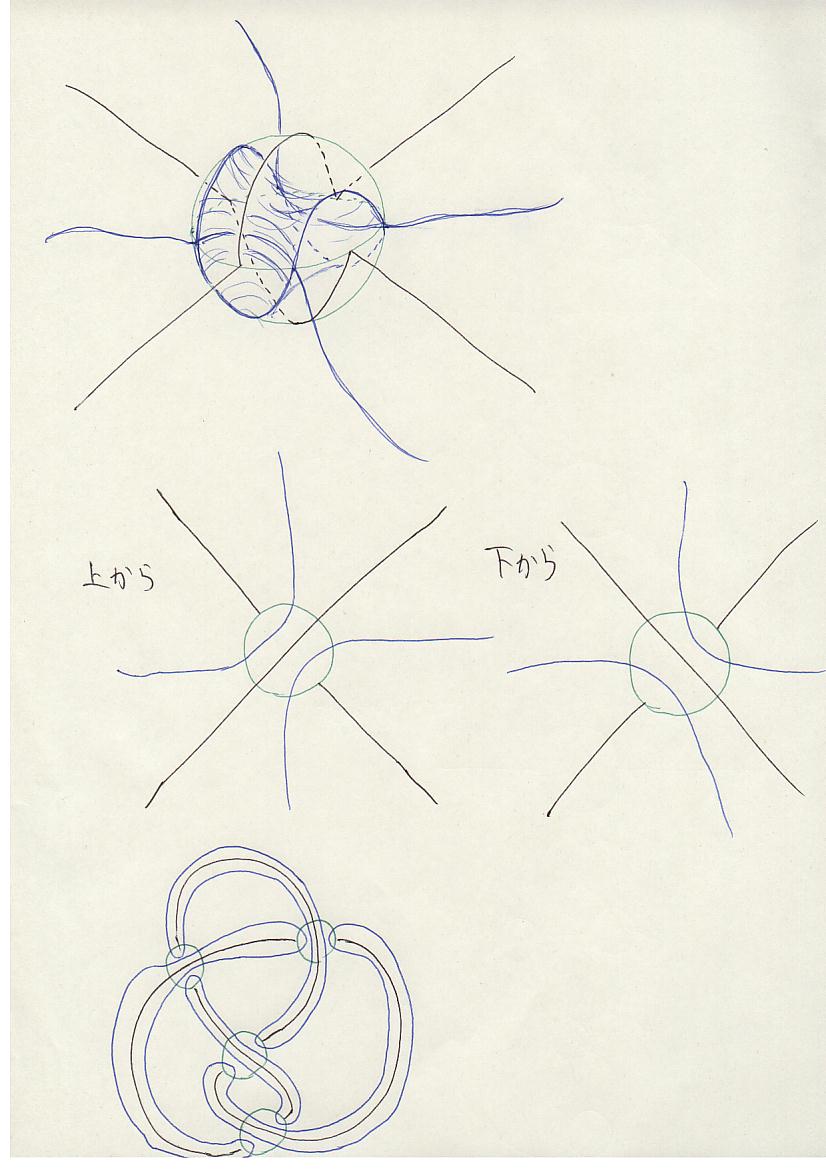
F ∩ S± のloopは、bubble を左右交互に横切る。
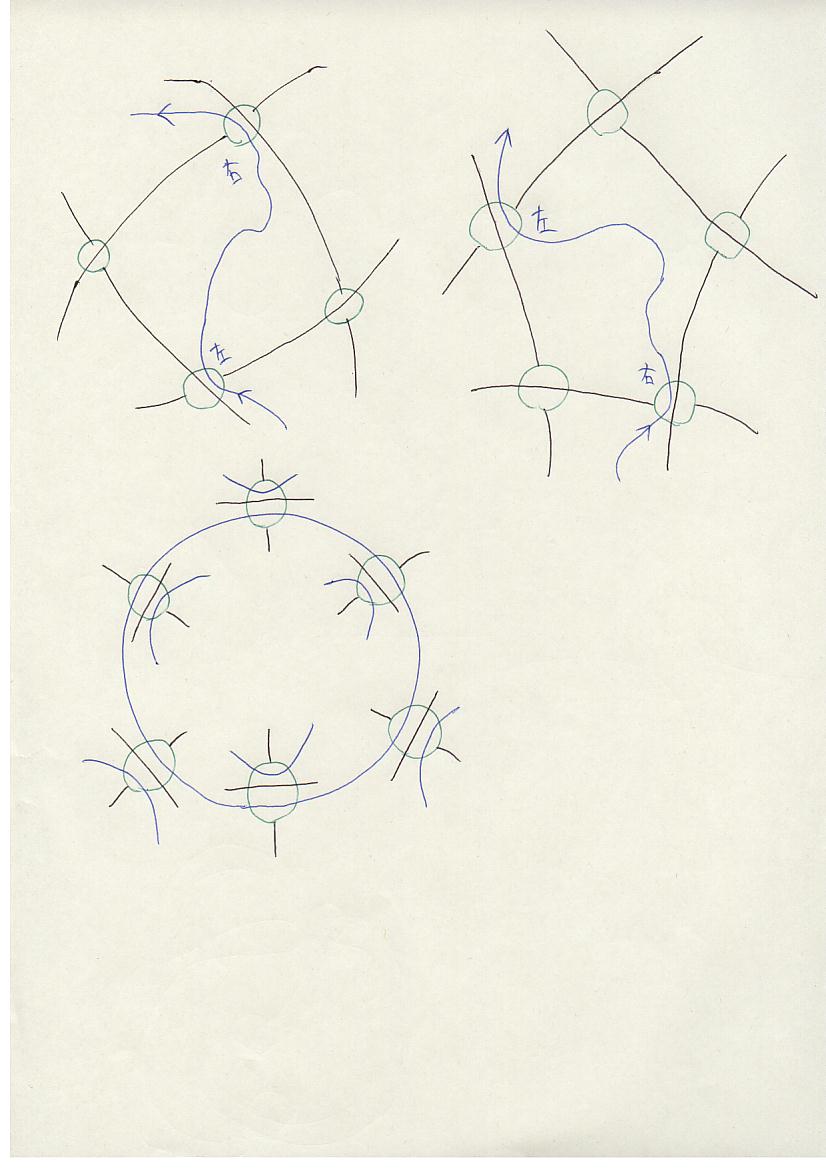
また、同じ bubble に戻ってくる loop は、下図のように F を変形することにより、消去できる。
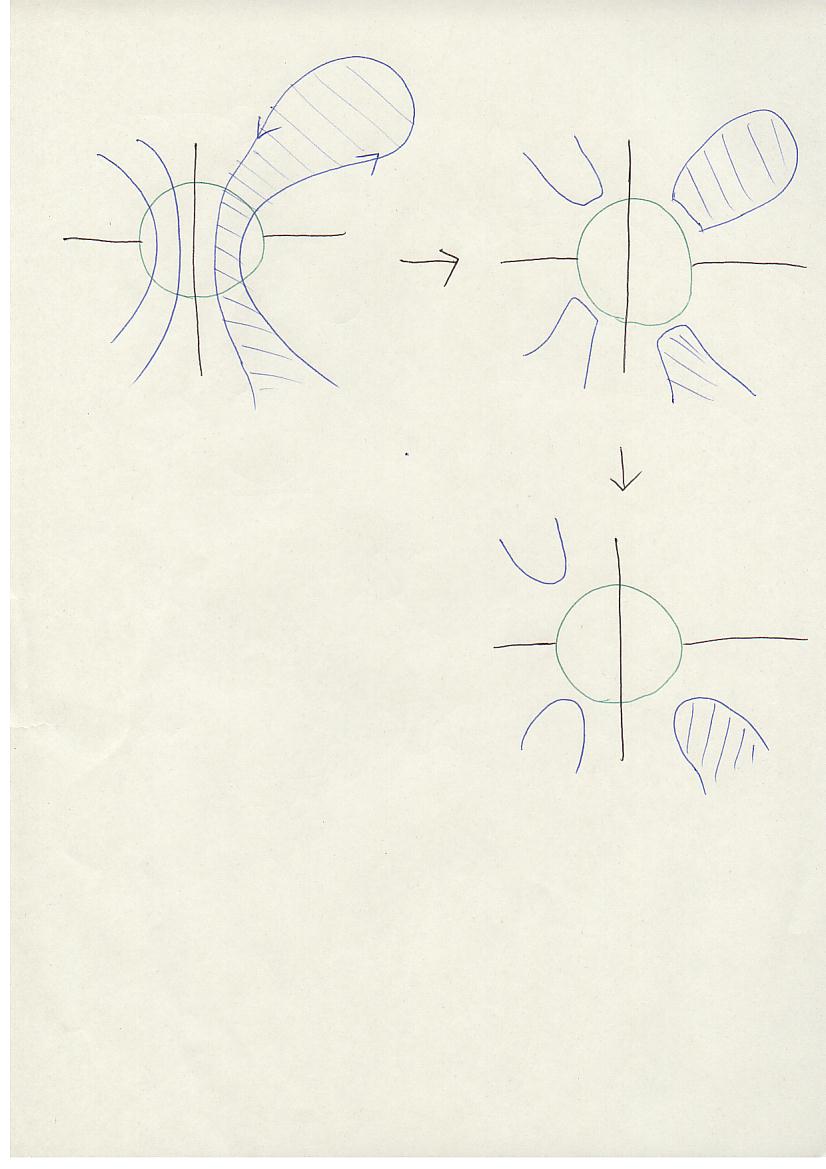
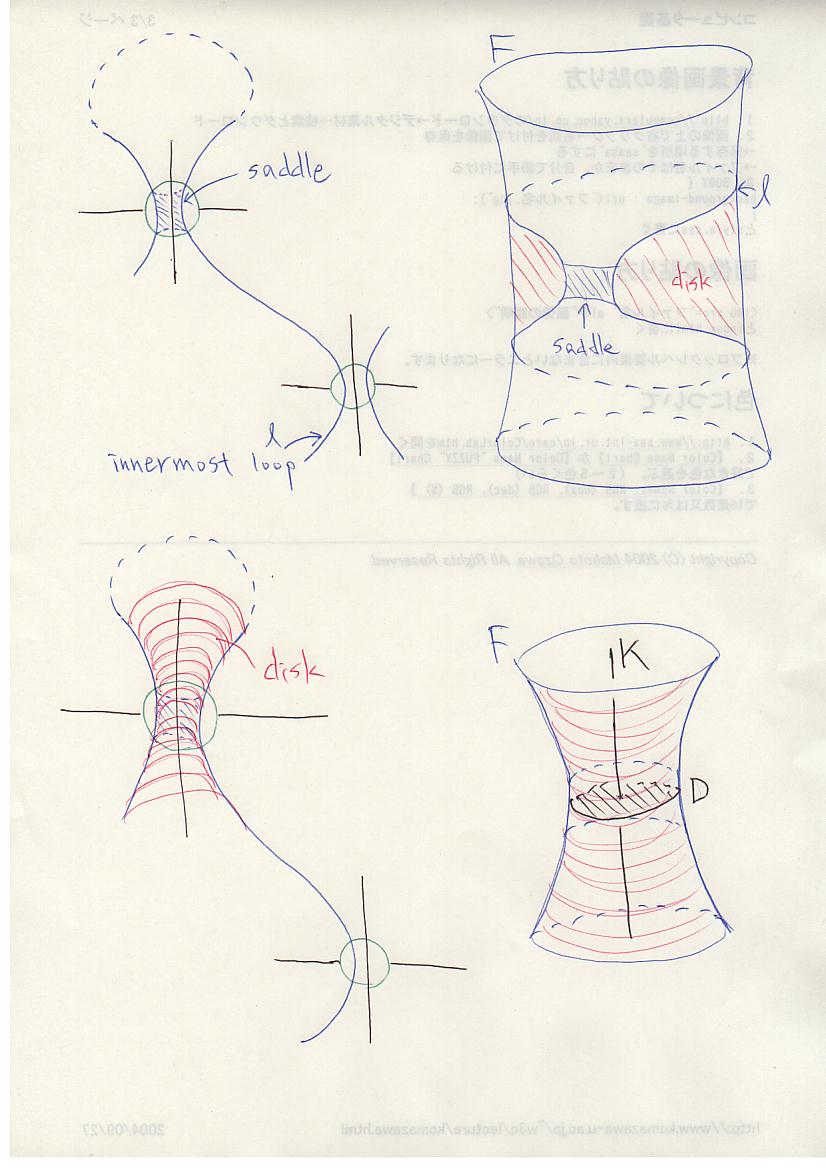
従って、F ∩ S± の S± 上でinnermostなloopは、同じ bubbleに戻ってこなければならない。
F ∩ B± は disk のみだったので、innermost loopに対応する F 上のdiskとsaddleの和に対して、定理の条件を満たすdiskが存在する。
交代結び目の既約な交代正則図形は最小正則図形であり、逆も成り立つ。
交代結び目の任意の既約な交代正則図形のねじり数は全て等しい。
交代結び目の任意の既約な交代正則図形は有限回の反転で移り合う。