表3.1の利得表で与えられる意思決定を、これから100日間に毎日おこなうとき、以下の各問に答えよ。
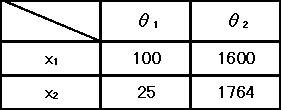
表3.1 利得表(単位ドル)
7 完全情報システムの期待価値と不確実性の評価
これまで述べてきた完全情報システムの期待価値を、別の観点、すなわち不確かな事前予想のもとでの選択(ないし決定)に関する不確実性の評価額、という観点から説明してみよう。
設例3.1[完全情報システムの期待価値と不確実性の評価]
表3.1の利得表で与えられる意思決定を、これから100日間に毎日おこなうとき、以下の各問に答えよ。
表3.1 利得表(単位ドル)

(1)今後の100日間をθ1=50日、θ2=50日と予想するとき、x1とx2のいずれの行動を選択するか。そのとき、100日間の予想される利得を求めよ。
(2)完全情報システムを100日間利用するときの期待利得と契約料金の上限額を求めよ。
(3)より一般に、今後の100日間をθ1=p×100日,θ2=(1−p)×100日と予想するとき、pを横座標に、完全情報システムの期待
(1日平均)利得(EMVPI)と期待価値(EVPI)を縦座標にして図示せよ。(4)★pの値が、p=1,0という極端な値をとるとき、EVPIの値を求めよ。また、そもそもp=1,0とは何を表しているかを吟味することによって、EVPIの値は何を表していると考えられるか。
EMVPI=Expected Monetary Value of Perfect Information(Expected Value with Perfect Information), EVPI=Expected Value of Perfect Information
8 不確実性のコストの2面的評価
論点8では、機会損失表をベースにして、選択に関する不確実性のより直接的な評価について説明する。そして、7での議論とあわせて「不確実性の2面的評価」ということを明らかにしてみる。
設例3.2[機会損失と不確実性のコスト]
先の設例3.1につき、
(1)機会損失表に基づいて、同じ問に答えよ。
(2)★ 設例3.1の(4)より、機会損失は何の尺度であると考えられるか。
9 リスク回避と完全情報システムの期待価値
これまでの議論は,意思決定者がリスクに対して中立であるということを前提にしていた。この前提をはずすと、以上の議論はどのように一般化され得るであろうか。
特に、これまでのリスク中立での議論をその中に含むより統一的な観点から、リスク態度を反映し、なおかつ効用ではなくこれまでと同様に金額でもって不確実性を評価するにはどのようにすればよいであろうか。
設例3.3[リスク回避と完全情報システムの期待価値]
意思決定者が効用関数U(π)= π 1/2(πは金額単位の利得)で表されるリスク回避者であるとき、
(1)このリスク回避者にとって、x1かx2の判断基準として、設例3.1でのリスク中立者の期待利得に相当するものは何か。
(2)リスク中立者の図3.1(完全情報システムの期待価値)に相当するものを、(1)に基づいて図示せよ。
10 リスク回避と不確実性のコスト
先の論点9が論点7のリスク態度を軸にした拡張の議論であったのに対し、論点10では論点8の拡張の議論をおこなう。すなわち、リスク回避における不確実性のより「直接的」な評価について説明しよう。
設例3.4[リスク回避と不確実性のコスト]
同じく、意思決定者が効用関数U(π)= π1/2(πは金額単位の利得)で表されるリスク回避者であるとき、
(1)このリスク回避者にとって、x1かx2の判断基準として、設例3.1でのリスク中立者の期待機会損失に相当するものは何か。
(2)リスク中立者の図3.2(不確実性の評価額)に相当するものを、(1)に基づいて図示せよ。
問題集に戻る